Статьи
Главная страница
Карта сайта

Методика обучения решению задач.
Решение задач как средство развития мышления учащихся

Можаев Г.М.
Тюменский государственный университет,
Тюменский областной институт развития регионального образования.

Одной из важнейших функций решения химических задач является развитие мышления учащихся. В самом деле, навыки решения конкретных химических задач потребуются в дальнейшем очень небольшой части выпускников средней школы. Но те или иные жизненные задачи будут возникать перед каждым из них, и способность решать их будет определяться общим развитием ученика, что закладывается на школьных уроках, в том числе и уроках химии. Таким образом, обучая решать задачи, надо стремиться не столько сформировать у ребят знание отдельных частных алгоритмов, сколько обучить их общему подходу к решению любой жизненной проблемы.

Осознанная человеческая деятельность, направленная на достижение некоторой цели, включает в себя следующие этапы:

- анализ ситуации:

- планирование;

- выполнение намеченного плана;

- осмысление результата, коррекция или переход к следующему витку деятельности, постановка новых целей.

Из этих этапов в обычной практике решения задач наиболее отчетливо проявляются два: анализ ситуации (он обычно распадается на два пункта – анализ количественных характеристик и анализ химической стороны задачи) и операционный этап, этап выполнения некоторой последовательности вычислительных действий. Многие учителя обучение решению задач понимают как выработку навыков операционного этапа, которую строят по алгоритмам, по образцам.

Сначала этот образец или алгоритм дается учителем как нечто готовое, затем таким образцом служит ранее решенная задача, алгоритм или решение подобной задачи, представленные на дидактической карточке и т.п. Не отметая полезности таких приемов в принципе, следует, однако, признать, что они сводят ученика до положения биоробота. Мыслительные операции ученика сводятся к тому, чтобы проанализировать условие задачи, выбрать один из знакомых алгоритмов и выполнить предписанный набор действий. Практически выпадает то, что собственно и отличает человека от компьютера: умение самостоятельно составить план, алгоритм, программу своей деятельности. Обычно выпадает (или сводится к простой проверке по последней странице учебника) и этап осмысления результата.

 На бездумное выполнение определенных действий нацеливает зачастую и контролирующая деятельность учителя. Что проверяется при решении учеником задачи на доске или в тетради? Конечный результат, или, в лучшем случае, «ход решения задачи» – то есть зафиксированная последовательность определенных операций. Насколько осознанно ученик использовал эту последовательность, как правило, остается за кадром.

Какой же из этапов деятельности по решению задачи наиболее важен с точки развития мышления? Конечно, наиболее творческий этап - этап планирования. Следовательно, именно этому этапу и надо уделить основное внимание при обучении решению задач: объяснять, обсуждать, контролировать. А для этого необходимо, чтобы план решения задачи как-то фиксировался и на доске, и в тетрадях учеников, и в разработках учителя. Описание словами неудобно из-за длительности, неоднозначности, малой наглядности. Вот если бы изображать план в виде схемы, используя при этом понятные всем условные обозначения…. Так в курсе географии отображается план местности, так в курсе физики из условных обозначений строятся схемы электрических цепей.

Статьи
Главная страница

[AD] -

Поделиться в

В этом суть методики структурного планирования:

-         разработать систему условных обозначений для элементарных вычислительных операций, используемых при решении большинства задач;

-         научить школьника разбивать задачу на отдельные структурные элементы, элементарные вычислительные операции;

-         научить изображать план решения задачи в виде наглядной схемы построенной из этих условных обозначений.

Система условных обозначений.

Порция вещества. Если не считать нахождения относительной молекулярной массы, то первые вычисления школьного курса химии связаны с величинами, характеризующими порцию вещества: массой, объемом, числом молекул и новой величиной - количеством вещества.

Из определения количества вещества прежде всего уясняется связь этой величины с числом структурных частиц (молекул или др.) через постоянную Авогадро. Затем устанавливается связь количества вещества с массой и объемом с помощью молярной массы или молярного объема.

Все эти взаимосвязи можно выразить общей формулой (1), а для их изображения на структурной схеме используется обозначение, называемое "куст расчетов для порции вещества" (рис. 1). Направление расчетов  показывается стрелками, так на рисунке 1 показано, что сначала по массе некоторой порции найдено количество вещества, а затем объем этого вещества в газообразном состоянии. В некоторых задачах масса и количество вещества используются для нахождения его молярной массы, т.е. основная "веточка" разворачивается в "листик" (рис. 1а).

Сложная система. Сложными называются системы, состоящие из двух или более компонентов: растворы, механические смеси, природные объекты и т.п. При описании таких систем кроме массы, объема, количества вещества, надо еще как-то характеризовать их состав. В школьном курсе химии для этого обычно используется величина "массовая доля" (формула 2).

Соответствующее условное обозначение называется "треугольник массовой доли" (рис.2), в котором по любым двум известным величинам можно найти третью. Аналогичен, хотя и реже используется "треугольник объемной доли" (рис. 2а).

Химическая реакция. Химическая реакция характеризуется, в первую очередь, своим уравнением, поскольку коэффициенты в этом уравнении показывают молярные соотношения участников реакции (формула 3). На структурной схеме уравнение реакции показывается волнистой линией, а нахождение количества вещества одного из участников реакции – стрелочкой под ней (рис. 3). Таким образом, расчет по уравнениям реакций ведется, как правило, в единицах количества вещества.

В расчетах по термохимическим уравнениям реакций используем пропорциональность между количеством вещества участника реакции и количеством теплоты (рис. 3а). Решая задачи на объемные отношения газов, учитываем пропорциональность их объемов (при одинаковых условиях) количествам вещества, и применяем формулу (3б), изображая ее стрелкой над уравнением реакции (рис. 3б).

Выход реакции. Выход реакции можно определить как отношение величины практически полученной порции вещества, к величине порции рассчитанной теоретически. Причем, поскольку это относится к одному и тому же веществу, безразлично, как характеризуется порция вещества: по массе, по объему или по количеству вещества (формула 4). По смыслу выход реакции близок к понятию “коэффициент полезного действия” реакции и его лучше обозначать буквой h (эта), которая применяется для обозначения кпд. Таким образом, получаем еще один треугольник - "треугольник выхода реакции" (рис. 4).

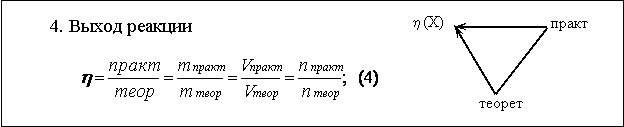Другие характеристики. В ходе решения задач ученик сталкивается и с другими характеристиками и вычислениями. Поскольку используются они не так часто, в ограниченном круге задач, то особых условных обозначений для них не вводится. Такие расчеты на схемах показываются обычными стрелками с минимально необходимыми пояснениями. Так на рисунке 5 показано применение абсолютной и относительной плотности, молярной концентрации, уравнения Менделеева-Клапейрона.

Таким образом, система условных обозначений включает в себя четыре основных элемента, но открыта для дополнений, позволяет показать любые другие необходимые действия.

Структурные схемы решения задач.

Поскольку основной величиной, используемой в химических расчетах, является количество вещества, то общий план решения большинства задач можно представить схемой 1: от исходных характеристик переходим к количествам вещества, проводим расчеты по формулам, уравнениям реакций и затем от количеств вещества переходим к требуемым величинам.

Составление детального плана решения задачи рассмотрим на примере достаточно сложной комбинированной задачи:

Определить объем этилена (н.у.), полученного из 150 мл 96%-ного этанола (плотность 0,8 г/мл) с выходом 65%.

1 этап - анализ количественных характеристик и краткая запись условия реакции. Учитываем, что 96%-ный этанол – это смесь этанола с водой – раствор, что отмечаем в краткой записи.

3 этап – план решения задачи.  При составлении структурной схемы можно начинать с разных сторон: с того, что дано, с того, что нужно найти, с каких то ключевых моментов. Например, характер рассуждений может быть следующим (одновременно зарисовываются элементы схемы 2):

Чтобы найти массу чистого этанола можно использовать массовую долю, но для этого сначала нужно найти массу раствора, используя объем и плотность (схема 2, действие 1). Затем, по треугольнику массовой доли находим массу чистого этанола (2.2). Для расчета по уравнению реакции переходим к количеству вещества, используя его связь с массой (рисуется куст расчетов 2.3). По уравнению реакции находим количество вещества этилена (2.4), затем, по второму кусту расчетов, его объем при н.у. (2.5). Найденное значение теоретическое, для того чтобы найти объем этилена, полученного практически, используем формулу выхода реакции (2.6).

При построении схемы «с конца» мы бы сказали, что для нахождения «практического» объема надо использовать «треугольник выхода» (2.6). Но для этого необходимо предварительно найти «теоретический» объем этилена, для чего нужно провести расчет по уравнению реакции и т.д.  Часто начинать планирование удобно с обсуждения того, какие расчеты по уравнениям реакций необходимы для решения задачи, и тогда построение схемы начнется с изображения волнистой линии и стрелки 2.4. Во всех случаях, разобрав план решения задачи, еще раз «пробегаем» его от начала до конца, если нужно - корректируем, нумеруем предстоящие этапы вычислений.

На схеме 3 показан фрагмент плана решения задачи, с несколькими расчетами по одному уравнению реакции, на схеме 4 – расчет по цепочке уравнений.

Наконец на схеме 5 представлен стандартный план решения задачи, когда одно из реагирующих веществ дано в избытке. Двунаправленная стрелка показывает в данном случае, что по любому из исходных веществ мы можем рассчитать необходимое количество второго вещества. Сравнив найденное значение с данным по условию задачи, определяем, какое из двух веществ прореагирует полностью (ПрП), по этому веществу ведем дальнейшие расчеты.

Не всегда нужно стремиться отразить на структурной схеме полное решение задачи. При решении сложных задач такая схема может получиться очень громоздкой или запутанной. В этом случае можно не показывать на схеме очевидные элементы, или планировать решение поэтапно, в виде нескольких отдельных схем.

Применение методики структурного планирования.

Условные обозначения должны даваться школьникам параллельно с изучением тех или иных величин. Желательно, чтобы они, так же как и основные формулы, были среди постоянных наглядных пособий кабинета химии. При решении простейших задач (нахождение количества вещества по массе, массы растворенного вещества и т.п.) зарисовываем на доске соответствующее условное обозначение, показываем стрелками направление расчетов, преобразование основной формулы. При переходе к более сложным задачам эти условные обозначения объединяются, образуя структурные схемы.

Ученики, слушая объяснение учителя, зарисовывают схемы в своих рабочих тетрадях. Учитель обращает внимание на то, что прогнозировать решение задачи нужно и при  самостоятельной работе в классе и дома. Проверка решения задачи может заключаться в обсуждении структурной схемы, представленной учеником, и правдоподобности полученного ответа (осмысление результата!). Подобное обсуждение может проводиться и в ходе групповой или парной работы школьников.

Можно существенно изменить содержание работы ученика над задачей, дав задание не решить ее, а проанализировать и составить план решения. Поскольку при этом снимается этап вычислений, за то же время ученик может проработать большее число задач, различных по своему строению или химическому материалу. Конечно, полностью отказаться от этапа вычислений тоже нельзя, поэтому задание может формулироваться так: «Проанализировать и составить план решения трех задач, одну из них прорешать».

Особенно оправданным становится этот прием при задании домашней работы массивом. Для сильных учеников, интересующихся предметом, здесь открываются дополнительные возможности по классификации и сравнению задач на основе их структурных схем, составлению задач определенного типа.

Задания «зарисовать структурную схему» могут использоваться и при проведении промежуточных контрольных работ. В то же время, готовя учеников к экзаменам и олимпиадам, надо объяснить, что структурная схема – только инструмент. Она применяется там, где необходима, может зарисовываться лишь на черновике. Нет смысла требовать от сильного ученика составления схем таких задач, которые он освоил до автоматизма. Здесь схема может понадобиться ему только в педагогических целях: чтобы наглядно показать ход решения задачи более слабым товарищам.

Подводя итог, можно отметить, что ценность структурных схем заключается в их возможности выполнять разные функции: быть средством анализа содержания задачи, методом планирования решения, опорным конспектом при объяснении учителем и учеником, основанием классификации и сравнения задач. Все это помогает реализовать и важнейшую функцию решения задач – развитие мышления учащихся.

Опубликовано: Можаев Г.М. Решение задач как средство развития мышления учащихся.
/Химия: Методика преподавания в школе, 2003, №3, с. 57-63.

Вернуться назад