12. Excel. Статистические функции. Графики. |
|||||||
ЗадачаИсследовательская работа связана с необходимостью правильно понимать и обрабатывать экспериментальные данные, оценивать влияние на них систематических и случайных ошибок. Случайные ошибки устранить нельзя, а также нельзя вывести никакой формулы для исправления полученного результата. В тоже время проведением повторных измерений и статистической обработкой полученных данных можно оценить величину этих ошибок и уменьшить их их влияние. Microsoft Excel предлагает большое число функций, облегчающих статистическую обработку данных эксперимента. Наша задача - обработать данные, приведенные в файлах Sil00.xls и Sil1.xls, с помощью этих функций, а также представить результаты эксперимента в графическом виде. I Запустите Excel, рассмотрите элементы рабочего окна. Откройте рабочие файлы. Скопируйте лист Ошибка из книги Sil00.xls в книгу Sil1.xls перед листом Данные. Сохранить как Фамилия-Sil-1.xls в папке НИТ на рабочем столе (тем самым создаем копию). Мастер функций (повторение)Вспомните основные приемы работы с Мастером функций. Запуск: кнопкой вставки функции fх. (или командой меню Вставка-Функция).
Выбор нужной функции. Все функции разделены на несколько категорий. На данном занятии в основном будут использоваться статистические функции. Выбрав нужную категорию функций, в списке функций (упорядоченном по алфавиту) находят нужную функцию. При щелчке по названию любой функции внизу появляется ее краткое описание. Специальная ссылка позволяет вызвать систему помощи Excel, в которой данная функция будет разобрана подробно, с примерами. Задание аргументов функции. Аргументами могут служить непосредственно данные или адреса ячеек, диапазонов ячеек, содержащих необходимые данные. Как правило, все исходные данные для функции должны быть на листе и вводят (указывая мышкой) адреса ячеек, содержащих эти значения. Обратите внимание, что окно аргументов можно перемещать, если оно заслоняет нужную часть экрана. Кроме того, рядом с полем для ввода есть маленькая кнопка с красной стрелочкой. При щелчке по ней окно аргументов сворачивается до узкой полоски, новый щелчок опять развернет окно аргументов. Помогает работе с мастером функций подсказка под полем для ввода аргументов, в которой разъясняется их смысл и возможные значения. Когда аргументы введены, в окне появляется значение функции, что тоже помогает избежать ошибок. Заканчивается работа с мастером функций нажатием кнопки "Ok" или клавиши "Enter".
I Запустите Мастер функций. Перейдите на категорию статистических функций, и просмотрите их список. Найдите функции СЧЕТ, разберитесь, используя подсказку, чем отличаются разные варианты этой функции. Счет значенийДля получения количества числовых ячеек в интервалах или массивах ячеек используется функция СЧЁТ. Использовать эту функцию удобно, особенно при большом числе данных, при их отбраковке.
Синтаксис: СЧЁТ(значение1; значение2; ...) где Функцию СЧЁТ можно вызвать через список функций значка АВТОСУММА (команда Число). I Лист Ошибка. В ячейке B14 введите формулу для подсчета числа экспериментальных точек. Проверьте работу формулы, удаляя/возвращая одно из данных (кнопка Отменить). Среднее значениеФункция СРЗНАЧ возвращает среднее арифметическое аргументов. Синтаксис СРЗНАЧ(значение1; значение2; ...), где Для подсчета среднего значения можно также использовать функцию УРЕЗСРЕДНЕЕ, которая вычисляет урезанное среднее, отбрасывая заданный процент данных с экстремальными значениями, чтобы исключить из анализа грубые ошибки, так называемые выбросы. Синтаксис: УРЕЗСРЕДНЕЕ(массив;доля), где I Лист Ошибка. В ячейках B15 и B16 введите формулу для среднего и урезанного среднего (доля 20%) значения. Проверьте работу формулы, удаляя/возвращая одно из данных (кнопка Отменить) Разброс точек. Дисперсия и стандартное отклонениеРазброс экспериментальных данных, оценивается дисперсией по выборке, которое определяется функцией ДИСП или стандартным отклонением (функция СТАНДОТКЛОН) Синтаксис: ДИСП(число1;число2; ...), или СТАНДОТКЛОН(число1; число2; ...) ДИСП и СТАНДОТКЛОН используют формулы: Стандартное (среднеквадратичное) отклонение - это мера того, насколько широко разбросаны точки данных относительно друг друга. Каждое измерение в данной серии (в данной выборке) отличается от другого в среднем на s. Понятно, что каждое отдельное значение оказывает влияние на средний результат. I Лист Ошибка. В ячейках B17, B18 введите формулы для дисперсии и стандартного отклонения выборки, в ячейках B19, B20 - формулы для дисперсии и стандартного отклонения среднего значения. Сохраните файл.
Критерий Стьюдента, доверительный интервалДля определения доверительного интервала, в который с заданной надежностью попадает измеряемая величина, используется критерий Стюдента t(a;f). Он был предложен в 1908 году англиским математиком и химиком Госсетом, который опубликовал их в работе под псевдонимом Student (студент). Для нахождения критерия Стюдента используется функция СТЬЮДРАСПОБР(a;f) . Синтаксис: СТЬЮДРАСПОБР(альфа;степень_свободы), где Функция СТЬЮДРАСПОБР использует метод итераций для вычисления результата. Если СТЬЮДРАСПОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д (не достижимо). Доверительный интервал среднего рассчитывается по формуле ДИ = ± sср*t(a;f) где sср - стандартное отклонение среднего. Если число измерений велико, можно использовать доверительный интервал для среднего генеральной совокупности, который находится с помощью функции ДОВЕРИТ, однако эта функция дает заниженные результаты при небольшом числе измерений. I Лист Ошибка. Введите формулы для расчета коэффициента Стьюдента и доверительного интервала (двумя способами). Рассчитайте относительную ошибку. Снесите окончательные результаты (формулами ссылок) в ячейки С26 и Е26. Отформатируйте их до оптимального числа значащих цифр. Линейная регрессияКоэффициенты линейной регрессии Y = mX+b и их ошибки вычисляются по довольно сложным формулам (рассмотренным на прошлом занятии). Excel предлагает ряд функций, облегчающих эти расчеты. Коэффициент m (наклон) линии, описываемой уравнением Y = mX+b может быть получен при помощи статистической функции НАКЛОН. Коэффициент b, показывающий отрезок, отсекаемый линией Y = mX+b на оси Y, может быть определен с помощью функции ОТРЕЗОК. Коэффициент корреляции Пирсона R, который отражает степень линейной зависимости между двумя множествами данных, и его квадрат (коэффициент детерминации) может быть получен с помощью функций ПИРСОН и КВПИРСОН. Синтаксис: I Лист МНК. Введите формулы для рассчета коэффициентов линейной регрессиии и коэффициента корреляции R2 для зависимости Y(dG) от Х(T). Сравните с данными полученными ранее, оцените приемлемость линейной модели. Полная статистика линейной регрессии. Формулы массиваНаиболее полную статистическую информацию по линейной регрессии выдает функция ЛИНЕЙН. Кроме того, эта функция позволяет обрабатывать данные по линейным функциям нескольких переменных (многофакторный эксперимент). Поскольку функция возвращает не одно значение, а несколько, массив значений, она относится к формулам массива. Ввод этих формул имеет ряд особенностей:
Синтаксис: ЛИНЕЙН(извест_знач_y; извест_знач_x; конст; статистика) В ячейке Е7 находится коэффициент m (наклон) линии, в ячейке F7 - коэффициент b (отрезок); I Еще раз прочитайте как вводятся формулы массива. Адекватность моделиДля определения уровня надежности модели нужно сравнить значения специального I Лист МНК. Найдите F-критерий и определите адекватность линейной модели. Графики: построениеОдной из важных и полезных возможностей Excel является возможность построения разнообразных графиков и диаграмм. В практике химического эксперимента чаще всего исследуется зависимость одной величины от другой. Такая зависимость может быть представлена точечным графиком. Построение графика.
I Лист МНК. Постройте точечный график зависимости Y(dG) от Х(T), поместив его на лист Результат. Редактирование графикаПолученный график не всегда сразу имеет удовлетворительный вид. Однако Excel позволяет в любой момент изменять его характеристики. Прежде всего, можно пермещать график, изменять размеры графика, как и любого графического объекта. Для этого его надо выделить и растянуть/уменьшить до требуемой величины. Щелкая правой кнопкой мыши по различным элементам графика (области построения, осям, линиям, точкам, надписям), мы открываем контекстное меню, позволяющее переходить к изменению их вида или удалению. Так можно изменить тип диаграммы, массивы данных, шкалы и подписи осей, цвета линий и заливки и т.д. Некоторые параметры диаграммы можно изменять, выделяя нужные элементы (или всю диаграмму) и используя кнопки на панели форматирования.
I Лист Результат. Отредактируйте график, добавьте название, установите оптимальные шкалы и форматы чисел, выделите маркеры экспериментальных точек синим цветом, используйте градиентную заливку. Сохраните файл. Линия тренда и дополнительные данныеЕще одной возможностью получить параметры линейной зависимости является построение линии тренда. Для этого щелкают правой кнопкой по точке графика и выбирают команду Добавить линию тренда. На вкладках этой команды выбираем тип тренда (линейный) и его параметры. В частности, отмечаем Выводить уравнение, Выводить коэффициент R^2. Открыв через контекстное меню точки окно "Параметры рядов данных", на график также можно нанести планки погрешностей, используя значение ошибок
I Лист Результат. Отредактируйте график, добавьте на него линию тренда и ее параметры, а также планки погрешностей. Сравните коэффициенты уравнения тренда с ранее найденными значениями. Сохраните файл. Дополнительный материал: |
|||||||
| . |
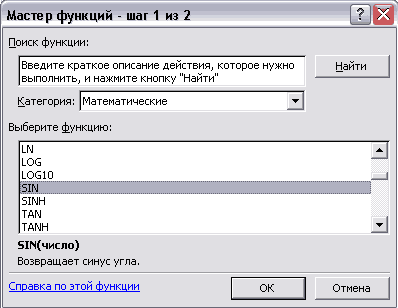
 Для работы с функциями можно использовать вкладку Формулы, где представлена библиотека функций, разбитая на категории. Можно прийти к вставке функций и через значок Автосумма, выбрав там команду Другие функции.
Для работы с функциями можно использовать вкладку Формулы, где представлена библиотека функций, разбитая на категории. Можно прийти к вставке функций и через значок Автосумма, выбрав там команду Другие функции. 
 - В Excel-2007 нет мастера диаграмм. Первый этап выполняется с вкладки Вставка. При этом на листе сразу появляется выбранный тип диаграммы.
- В Excel-2007 нет мастера диаграмм. Первый этап выполняется с вкладки Вставка. При этом на листе сразу появляется выбранный тип диаграммы.
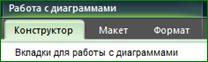 При щелчке на диаграмме появляются три дополнительные вкладки Ленты, предназначенные для работы с диаграммами. На вкладке Конструктор можно изменить тип диаграммы, определить исходные данные,
При щелчке на диаграмме появляются три дополнительные вкладки Ленты, предназначенные для работы с диаграммами. На вкладке Конструктор можно изменить тип диаграммы, определить исходные данные,
 если они не были выделены предварительно, выбрать макет, стиль и размещение диаграммы. Вкладка Макет позволяет проводить более детальную работу с элементами диаграммы (Легенда, Название, Подписи, Сетка, Оси и т.д.) Вкладка Формат предоставляет дополнительные возможности форматирования объектов диаграммы.
если они не были выделены предварительно, выбрать макет, стиль и размещение диаграммы. Вкладка Макет позволяет проводить более детальную работу с элементами диаграммы (Легенда, Название, Подписи, Сетка, Оси и т.д.) Вкладка Формат предоставляет дополнительные возможности форматирования объектов диаграммы.